Find a compact metric space that does not embed in for any
.
- Comment
- Reblog
-
Subscribe
Subscribed
Already have a WordPress.com account? Log in now.
Find a compact metric space that does not embed in for any
.
Consider the subspace of
of 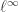 of all sequences
of all sequences 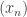 such that
such that ![x_n \in [0, 1/n]](https://s0.wp.com/latex.php?latex=x_n+%5Cin+%5B0%2C+1%2Fn%5D&bg=ffffff&fg=333333&s=0&c=20201002) . It is easy to see that
. It is easy to see that  is compact, since it is closed in
is compact, since it is closed in 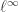 and totally bounded.
and totally bounded.
On the other hand, for any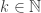 the convex hull of the points of the form
the convex hull of the points of the form  with
with  and
and  is contained in
is contained in  . In other words, we can embed a
. In other words, we can embed a  -simplex in
-simplex in  for all
for all  , so
, so  has infinite topological dimension, and therefore does not embed in
has infinite topological dimension, and therefore does not embed in 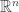 .
.
LikeLiked by 1 person
Consider the countable product of copies of![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) . This is metrizable and compact, but doesn’t embbed in any Euclidean space by the same argument above. (This is homeomorphic to the example given above, in fact.)
. This is metrizable and compact, but doesn’t embbed in any Euclidean space by the same argument above. (This is homeomorphic to the example given above, in fact.)
LikeLiked by 1 person